I’m teaching my own math class this semester! The good people at the New York City College of Technology Adult Learning Center (City Tech, for short) set up a Monday night math class for me so that I could get back into the classroom. For the last three years, I have been supporting teachers by doing workshops and writing curriculum, and I’ve benefited from learning from amazing colleagues and teachers. I’ve been able to teach some math and science lessons as a guest teacher over the years, but I’ve been itching to try out curriculum and practice teaching strategies over the course of a semester.

When I was a full-time classroom teacher, I was hungry for staff development and materials, but I sometimes found it difficult to put materials together in a coherent way across a semester. For the class I’m teaching now, I really wanted to make most of the major decisions in advance, while remaining flexible to respond to how each class goes. Having the CUNY HSE Math Framework in Functions and Algebra is a huge help, but planning a semester is still really challenging. I have 13 three-hour classes and multi-level class. How far will I be able to get? How much other work on foundational skills, number sense, subjects other than functions, etc. will I need to weave in? How do I pull from the many resources collected in Framework Posts?

Mark Trushkowsky, my close colleague and friend at the CUNY Adult Literacy/HSE Program, is supporting me in the class. We talk before and after each class and Mark has been visiting as a tutor and observer when he can. We also have a fantastic tutor, Celeste Faaiuaso, from City Tutors as well. It’s a little scary to have people observing you teach each class, but it’s been really helpful. I really want to learn to open my teaching to whoever wants to observe at any time. That feels like the best path towards helping me see blind spots and improve my teaching.

Functions and algebra have been the focus of our recent work, but this is my first time teaching the Framework. Since functions and algebra make up more than half the HSE exam, if students learn the skills in the functions and algebra lessons in the Framework, we feel that students will have a much better chance of earning their HSE diploma. As part of our discussions about improving the HSE math pass rate, Mark and I have recognized the need to make the Framework more accessible to a range of teachers. One of our goals with the class is to develop a semester plan that can be used by other teachers. We want to show how teachers might incorporate lessons from the Framework, visual patterns, instructional routines and other resources from the Framework Posts. We’re hoping that this model, possibly with other supports, could help more teachers take advantage of these lessons and teach content that is on the test.

Here’s an outline for my first class a few weeks back:

• Sequences 1.1
• Name Race
• Letter to students
• One question interviews
  • Math is…
  • Math can be difficult because…
  • One way to help ourselves understand math better is…
• Upside Down T Visual Pattern
• Reflection: What would be a good title for tonight’s class? Describe the class. What do you want to learn more about?
• Pick a number 1-10. How was tonight’s class? Volunteers share explanation.

For homefun (explanation below), I gave out:

• Sequences 1.2
• The Upside Down Problem, part 3

After class, I took some notes on what went well and what could have been better:

What are 3 words to describe tonight’s class? Humbling, heart, optimism.

Successes: The group bonded. The Name Race was fun. The goal is to see how quickly we can all say our own names (see description above). I had a stopwatch out and was about to start. Then, Christopher walked in without knowing what we were doing and was immediately charming. Everyone raced around the circle saying their name as quickly as they could. It got to him and he said, “Hiiii, myyyy naaaame issss Chrisssstopheeeer. Hooow arrre yoooou dooooing?”

Students engaged with the activities. They walked around and talked to each other. They asked each other’s names and starting quizzing each other later. There was a lot of laughter. A few people opened up about how they struggle with math. They seem excited to work together.

Their ideas for learning math were great: Practice, study, research, ask questions, communicate, attend class regularly, be active, work hard, help each other, be open-minded to new techniques, do your homework (I changed this to homefun, then trainfun when people said they could do schoolwork on the train, but weren’t sure when else they could work on it.)

Challenges: I skipped so much of the lesson plan. I had to skip the algebra and patterns conversation. I forgot to debrief the Name Race activity. I forget almost a page of my notes…

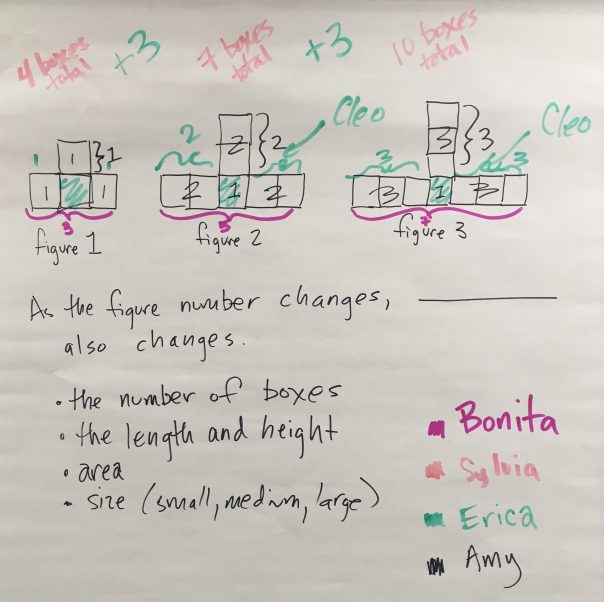
I got a bit lost in the debrief of the Upside Down T visual pattern. I merged a couple conversations: “As the figure number changes, the ____ also changes.” and labeling the change that people saw (Bonita, Selvija, Erica and Amy’s ways of seeing).

Most people saw the figure as a horizontal row of 3, 5, 7, 9… and a vertical column dropped on top of that horizontal row. I didn’t use it when I was trying to help the class get to a generalization (3n + 1). It probably would have been easier to get to a generalization using this way of seeing, but I wasn’t prepared for it. It might be useful for me to think about how I would structure this conversation the next time if students saw it in this way:

fig. 1 –> 3 + 1
fig. 2 –> 5 + 2
fig. 3 –> 7 + 3
fig. 4 –> 9 + 4
fig. 5 –> 11 + 5

How do you figure out the number of squares in the horizontal part? Ask different students to explain. At some point, I would expect some one to say that the number on each side of the vertical column is the same. And how many are there on each side?

What do you notice? What’s changing? What’s staying the same? … Eventually getting to the expression (2n + 1) + n for the number of squares in the nth figure.

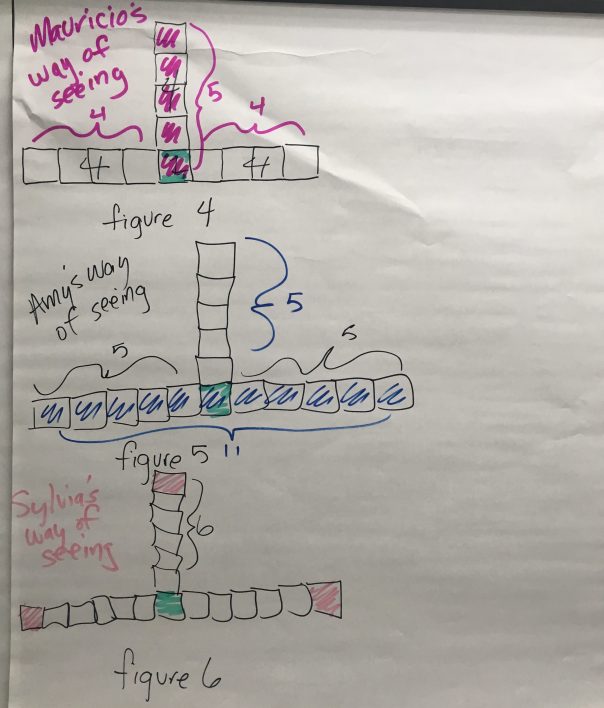
It was also challenging to get around the class while they were drawing the 4th and 5th figure in order to see what way of seeing they might be using. I thought Mauricio had drawn one center square, then three legs, but when I asked him share how he saw figure 4, he drew five vertical, then four on either side. When I ask Amy how to draw fig. 5, she drew 11 horizontal, then five going up.

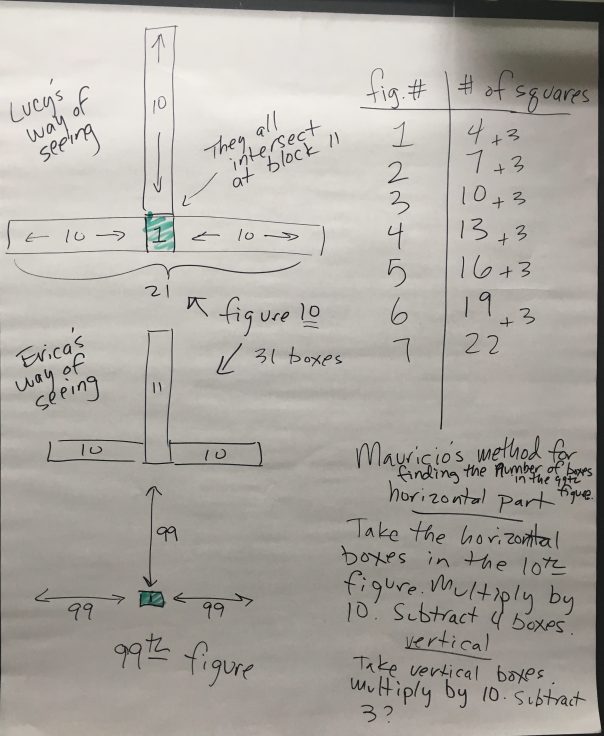
I also had trouble helping them move from the 10th figure to the 99th figure. I didn’t think to have them talk to each other. I’m now realizing that a pair/share at a challenging moment can be a way to get some new ideas communicated or a misconception corrected.

I think they had the tools after the 10th figure, but needed more time to process in small groups. We got the 99th figure, but it took a lot. We had to go back to the 1st, 2nd, and 3rd figures, and then add a middle square that Cleo noticed. Counting the length of the legs off the middle square helped get to a generalization, but I was pushing this way of seeing pretty hard.

For me to think about:

• What is the reason for the steps of the group debrief of the visual pattern? I had students help me draw different figures and labelled their ways of seeing, but I had trouble asking other students to use another student’s way of seeing. I really need to read 5 Practices for Orchestrating Mathematical Discourse.
• This class would love the Handshake Problem. I can imagine them acting the whole thing out. It would take a while, but could be really fun. 

I hope to share a blog entry at least once every few weeks on the class. Comments welcome.